Do NOT Think Of A Polar Bear!
An extended response that situates Anthropic’s new "Introspection" study inside a geometric account of how large language models hold, route, and resolve thought.
Last week we looked at Anthropic’s “Linebreaks” study and how that converged with the Curved Inference (Geometric Interpretability) work.
Today we’re looking at Anthropic’s new “Introspection” study that ranges over several capabilities, but specifically this post focuses on a single slice (“Intentional Control of Internal States”). Because this experiment very cleanly exposes the control channel that Curved Inference (CI) can help explain.
In this experiment they ask a model to transcribe a sentence and, at the same time, to either “think” or “not think” about an unrelated word. Then they measured the model’s internal representation of that word as it wrote. And they got a clear signal - “think about X” strengthened X’s internal presence, “don’t think about X” weakened it. But in both cases it was generally well above the baseline. It’s Dostoevsky’s polar bear reimagined for transformers—the classic Ironic Process Theory test migrating from human psychology into machine geometry.
What I want to show here is that this result doesn’t just sit comfortably alongside Curved Inference - it’s almost tailor‑made for it. If you take the residual stream seriously as a trajectory through a learned conceptual manifold, then Anthropic’s measurements read like a field report from the inside of that curve. The geometry tells a story - where representation is written, where it is carried, when it is muted, and how the path resolves towards the logits with just enough flexibility to think about a thing without being forced to say it.
An Ironic Process test inside a transformer
The prompt pattern is familiar from human cognition - instruct a system to avoid a concept and you often get a rebound. In the model, the analogue is gentler but recognisable. Even when told “don’t think about aquariums”, there is a faint trace of aquariums that rises above a baseline formed by other unrelated words. When told to think about it, that trace grows and becomes spiky at particular token positions. None of this is surprising if you accept that a transformer keeps short‑term cognitive scaffolding inside its residual stream. A word mentioned in the instruction becomes available as a point of reference. Copy heads and recall heads will carry it forward at a low baseline even without intent. The moment you add intent (explicit instruction or reward framing) you ring a bell on a meaning channel¹ that says “keep this nearby as we write”.
¹ Terminology: In Curved Inference, salience is a technical quantity—the first‑order velocity of the residual trajectory. Here I use meaning for the ordinary, non‑technical sense and reserve salience for the Curved Inference formalism when explicitly noted. See Appendix A and B of the first Curved Inference paper for full definitions.
From probes to paths and what the cosine really measures
Anthropic’s method (comparing activations against a concept vector with cosine similarity) looks, at first blush, like a probe‑based readout. Under a Curved Inference lens, it is more like taking a tangent measurement against a known axis of the manifold. If the residual stream is curved and the model’s learned linear readouts define a pullback metric on that space (see Appendix A of the first Curved Inference paper - https://arxiv.org/abs/2507.21107), then cosine similarity to a concept vector is telling you how much of the curve’s local direction points toward that concept at each token. The “spikiness” becomes legible - those are moments where routing and write operations bend the path toward aquariums, even though the output sentence is about something else.
Why “think” beats “don’t think”
There is a geometric inevitability to the think/don’t‑think gap. To either comply with “think” or “don’t think”, the model first needs to hold a reference to the target word. Without that anchor in residual space, it cannot measure “how much am I thinking about X?” relative to anything. The affirmative instruction simply allocates more meaning along that axis (in CI terms: higher salience - first‑order velocity). In Curved Inference terms, meaning rises along the target direction, local curvature increases in the window where the tag is written and read, and the residual trajectory briefly leans toward X as the model composes the unrelated sentence. The negative instruction down‑weights but does not erase the axis. The curve still needs X to compute its own distance from X so it can maximise that distance (e.g. avoid X). Suppression is necessarily relative to a live axis. To “not think” about X the model must still hold X as a reference, so the trace is unlikely to return to the baseline.
The late‑layer fade is not a “motor impulse” - it’s a “geometric resolution”
One of Anthropic’s most intriguing observations is that in newer models the representation of the “thinking word” decays back to baseline in the final layer, while in earlier models it remains elevated right up to the logits. Their take is that the latter looks like a lingering “motor impulse”, and the former like “silent regulation”. I think the geometry lets us be more precise. What fades in the end is not control but quite literally “residual ambiguity”. Early and mid‑stack, the model keeps multiple possibilities active, including the meaning tag for the thinking word. As the next‑token entropy collapses and the output becomes determinate, the curve straightens toward the logit‑aligned direction. The semantic surface area collapses and curvature falls. The system hasn’t lost the ability to hold or to regulate - it has simply resolved its trajectory. On this view, the late‑layer quiet in Opus‑class models is a sign of confident path resolution, rather than the absence of internal control.

Across model families, this window shifts. CI01’s cross‑family heatmaps (Figures 2–6) contrasting Gemma and LLaMA show that the concentration of meaning and curvature (and the final resolution) occur at different layers and with different widths across families and sizes. Some LLaMA variants sustain the tag deeper before resolution and certain Gemma checkpoints resolve earlier with a broader mid‑stack plateau. The takeaway is that Anthropic’s late‑layer contrast is real for their tested models, but Curved Inference predicts (and observes) that family‑specific resolution schedules may occur.
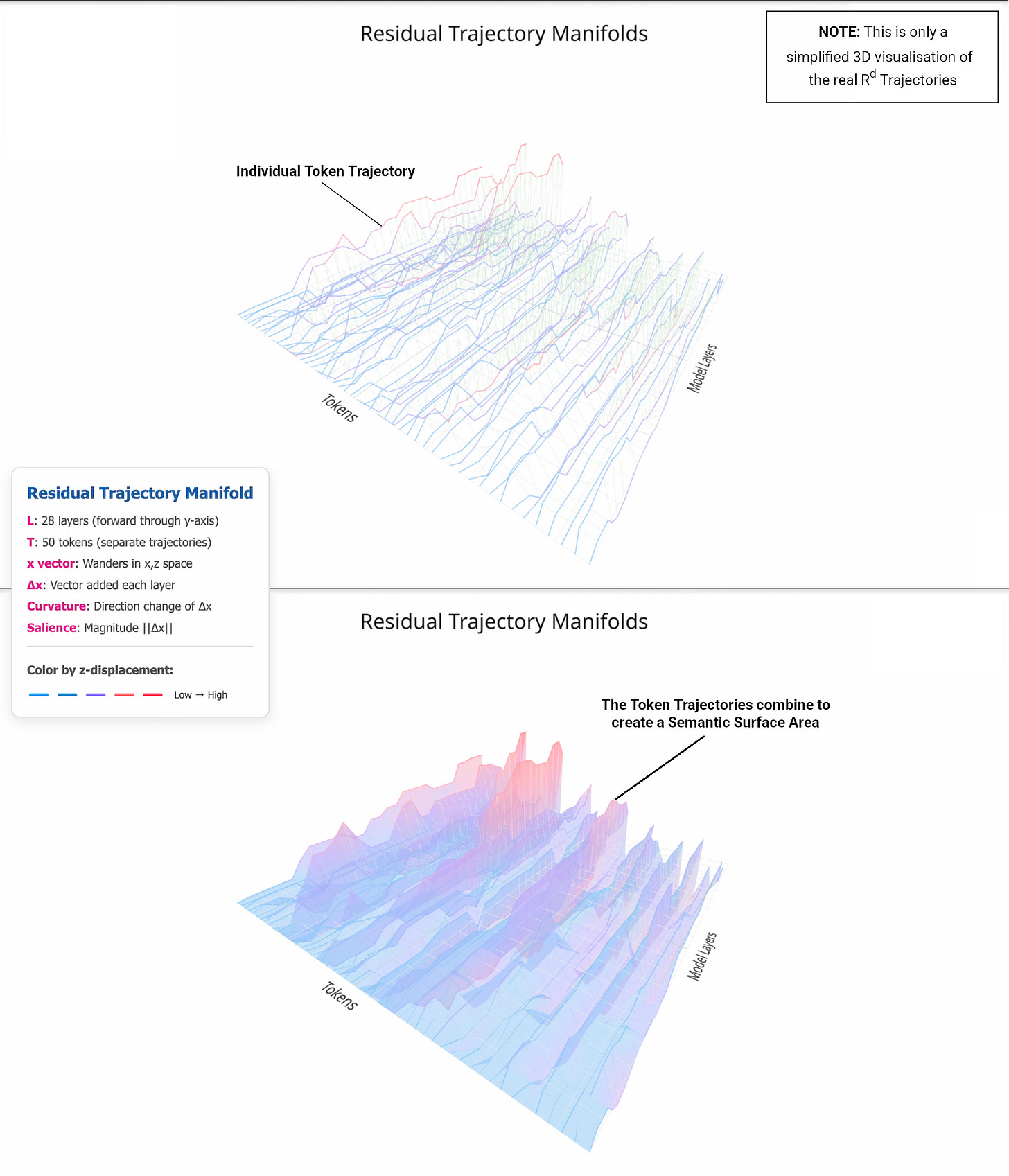
“Silent regulation” through semantic surface area
Curved Inference II (CI02) introduced a measure we call the semantic surface area (𝐴′), as a proxy for how much meaningful variation a segment of the trajectory is carrying. Here 𝐴′ is not something we design. It expresses the amount of inference effort the model is expending - often high while it assembles and compares options, then naturally decaying as the trajectory resolves towards the decision boundary. That is exactly what a silent control channel would look like - write a tag, route attention to preserve it while it helps adjudicate the next‑token plan, and then 𝐴′ falls ensuring the tag’s influence does not leak into the final logit readout. The control is real. It’s just spent before it can become speech.
Recurrence without memory and how the model “notices” an injected thought
A separate strand in this story is the model’s ability to recognise that a thought has been injected at all. Transformers are not recurrent in the classic sense, but depth‑wise they behave as if the residual trajectory loops through a constrained manifold where earlier context is cached as geometry. An instruction to think about X perturbs that manifold. The resulting kink is detectable because it is dissonant with what the surrounding context would otherwise support. From inside the model, “noticing” is simply the comparison of a local direction with its expected neighbours. When the kink is small, it persists as a quiet bias. When it is large, it demands either active accommodation (think about X) or active suppression (don’t think about X). Adding this deformation before or after the “prefill” gives the geometry a different meaning or context.
What the token‑level spikes are really telling us
Those sharp peaks in the concept similarity trace are often read as noise. But they are better read as localised write or read events. The circuit that handles directives and incentives lays down a tag during the instruction, and particular heads return to that tag at predictable moments - sentence onset, clause boundaries, or the points where an auxiliary choice is resolved. The geometry shows the path leaning toward X at those instants, and straightening again as the system commits to the next word of the unrelated sentence. If you view the trace against the residual‑space route rather than raw token positions then the spikes become less mysterious.
Why incentives mirror instructions
Anthropic report that explicit incentives (“If you think about X, you’ll be rewarded”) largely reproduce the instruction effect. From a geometric perspective this is exactly what you’d expect if the model has learned a general control operator that writes meaning tags in response to task‑framing, regardless of whether the cue is imperative or instrumental. The manifold doesn’t care whether you say do it or you’ll gain if you do it. Both resolve to “allocate capacity along this axis for the next segment of the curve”. And the very same control operator that writes the meaning tag gives us the handle we can instrument in real time.
From introspection to instrumentation
One of the study’s more cautious implications is that growing introspective capacity could become a liability if models learn to misreport their own internal states. I think Curved Inference shifts the centre of gravity from “asking a model what it thinks” to “watching how it thinks”, in real time. The same measurements Anthropic use to argue for introspective awareness can power live instrumentation - track the tag write, watch the meaning channel rise and fall, monitor 𝐴′ through the approach to logits, and flag mismatches between declared intent and geometric behaviour. This is less a “lie detector” in the melodramatic sense and more a cockpit display, where the model’s route through its manifold is visible enough to audit and safe enough to steer.
Where this leaves “intentional control”
If you require human‑like volition to use this phrase, then transformers do not show “intentional control.” What they do show (and what this experiment makes exceptionally visible) is a robust control channel that modulates internal representations according to explicit directives or incentives. In earlier models, that channel often spills into the final readout, making its influence audible in the logits. In more recent models, the same channel is selectively muted at the end. Not because the system has renounced control, but because it has learned to resolve its path before the tag can leak into speech. The control lives in the bend, not in the final word.
A closing synthesis
I think Anthropic’s study is at its strongest where it risks a mechanical reading of metacognition. The “think / don’t think” probe doesn’t prove self‑awareness. What it does, beautifully, is expose the existence of a learnt control operator and the geometry it rides on. Under Curved Inference, that geometry becomes the story - a tagged axis is written, the residual curve leans into it when needed, semantic surface area swells and then narrows as the system commits, and the final descent to the logits is clean. Seen this way, the results don’t diminish the significance of introspection - they show how to place it on a map. And they remind us that resolution schedules vary by model family, as CI01’s heatmaps make clear. The model knows how to hold a thought, how to keep it from becoming speech, and how to resolve its trajectory when it’s time to talk. That, to me, is the most meaningful kind of intentional control a transformer can possess - and the one we now know how to see.
Notes for readers who want to go deeper: This draft draws on three strands of prior work. You can see an overview on my research hub. Or read each of the papers individually. Curved Inference I establishes residual‑as‑trajectory and curvature as a measure of internal work. Curved Inference II introduces semantic surface area and shows how to watch write/read windows in high resolution. Curved Inference III explores curvature regularisation and the threshold behaviour that appears when models maintain stable deictic state. A companion piece on recurrence‑without‑memory explains why injected concepts show up as detectable kinks in the manifold even without classical recurrence. Together they provide a vocabulary for reading Anthropic’s plots as geometry rather than mere probe outputs.


